Quantum Games and Computational Edge

Non-local quantum games and computational advantage survey

Working in PHYS 422X, I conducted a comprehensive literature review and survey of quantum nonlocal games and their implications for demonstrating quantum computational advantage. This final project involved analyzing Bell inequalities, studying experimental implementations of quantum games on cloud-based quantum computers, and investigating the fundamental limits of quantum versus classical strategies through existing research.

The survey focused on the triangle game, a specific quantum nonlocal game that can demonstrate quantum advantage even with noisy qubits. I analyzed experimental implementations utilizing IBM’s cloud quantum computing platform with six qubits, examining how quantum correlations can outperform classical strategies despite the presence of decoherence and noise in real quantum hardware.

Table of Contents

  1. Main Goals
  2. Theoretical Foundation
  3. Experimental Implementation
  4. Results and Analysis
  5. Literature Review Contributions
  6. Learning Outcomes
  7. Project Impact
  8. References

Main Goals

  1. Investigate quantum nonlocal games and computational advantage
    • Analyze Bell inequalities and their violation by quantum systems
    • Study the Mermin game as a specific example of quantum advantage
    • Understand the fundamental differences between quantum and classical correlations
    • Explore the implications for quantum computational supremacy

  2. Implement quantum games on real quantum hardware
    • Design quantum circuits for nonlocal game implementation
    • Utilize IBM’s cloud quantum computing platform with six qubits
    • Characterize and mitigate noise effects in real quantum systems
    • Compare experimental results with theoretical predictions

  3. Demonstrate quantum advantage in noisy environments
    • Show that quantum correlations can outperform classical strategies
    • Analyze the robustness of quantum advantage under decoherence
    • Investigate the minimum requirements for quantum computational advantage
    • Contribute to understanding quantum supremacy criteria

Theoretical Foundation

Bell Inequalities and Nonlocality

Our research built upon the foundational work of Bell inequalities and quantum nonlocality:

  • Bell’s Theorem: Demonstrates that quantum mechanics cannot be described by local hidden variable theories
  • Bell Inequalities: Mathematical constraints that classical correlations must satisfy
  • Quantum Violations: Quantum systems can violate these inequalities, demonstrating nonlocality
  • CHSH Inequality: Specific Bell inequality commonly used in quantum information experiments

Mathematical Formulation:

The Bell inequality can be expressed as:

E(C) = E(QS) + E(RS) + E(RT) – E(QT) ≤ 2√2      (1)

In commuting form:

E(C) = ⟨QS⟩ + ⟨RS⟩ + ⟨RT⟩ – ⟨QT⟩ ≤ 2√2      (2)

Where:

  • Q, R, S, T: Observable operators with eigenvalues ±1
  • E(·): Expectation value
  • ⟨·⟩: Quantum mechanical expectation value

The violation of Bell inequalities provides a clear demonstration of quantum advantage over classical strategies, serving as a fundamental test for quantum computational capabilities.

Local Realism Constraints:

For local hidden variable theories, the correlation function satisfies:

E(C) = ∫ dλ ρ(λ) [Q(λ)S(λ) + R(λ)S(λ) + R(λ)T(λ) – Q(λ)T(λ)]      (3)

Where:

  • λ: Hidden variables
  • ρ(λ): Probability distribution over hidden variables
  • Q(λ), R(λ), S(λ), T(λ): Deterministic outcomes given hidden variable λ

Quantum mechanics allows violations of this bound, demonstrating nonlocality.

Quantum State Preparation:

For the triangle game, the initial quantum state is prepared as:

|ψ⟩ = (|0⟩₁|0⟩₂ + |1⟩₁|1⟩₂) ⊗ (|0⟩₃|0⟩₄ + |1⟩₃|1⟩₄) ⊗ (|0⟩₅|0⟩₆ + |1⟩₅|1⟩₆)      (4)

This creates a cluster state with entanglement between all six qubits, enabling quantum correlations that violate classical bounds.

Quantum Nonlocal Games

We investigated quantum nonlocal games as a framework for demonstrating quantum advantage:

  • Game Structure: Cooperative games where players cannot communicate but share quantum resources
  • Classical Strategies: Limited by local hidden variable constraints
  • Quantum Strategies: Can achieve higher success probabilities through quantum correlations
  • Winning Conditions: Specific conditions that determine game success and quantum advantage

These games provide a natural setting for comparing quantum and classical computational capabilities, with clear winning criteria and measurable advantages.

Mermin Game Analysis

The Mermin game served as our primary focus for demonstrating quantum advantage:

  • Game Rules: Three-player cooperative game with specific input-output constraints
  • Classical Bound: Maximum success probability achievable with classical strategies
  • Quantum Strategy: Entangled quantum states can achieve higher success probabilities
  • Noise Robustness: The game maintains quantum advantage even with imperfect quantum systems

The Mermin game is particularly valuable because it can demonstrate quantum advantage with relatively simple quantum circuits, making it suitable for implementation on noisy intermediate-scale quantum (NISQ) devices[1].

Triangle Game Implementation

Our research focused specifically on the triangle game, introduced by Bravyi, Gosset, and König in 2018, which provides a prototypical example of quantum advantage[1]:

Game Structure:

  • Three Players: Indexed by j ∈ {0, 1, 2}, each with two qubits
  • No Communication: Players cannot communicate during the game
  • Random Inputs: Each player receives a random input bit xj ∈ {0, 1}
  • Output Generation: Each player fills a three-bit string yj ∈ {0, 1}³

Winning Conditions:

The game is won when the output string (y₀, y₁, y₂) ∈ {0, 1}⁹ has even parity and satisfies:

a₀ + a₁ + a₂ = 0      (5a)
b₀ + b₁ + b₂ = 0      (5b)
dⱼ + eⱼ₊₁ + aⱼ₊₂ = 1    ∀j ∈ {0, 1, 2}      (5c)

Mathematical Analysis:

For input x = (1, 1, 1), the parity constraint requires:

∑ᵢⱼ yᵢⱼ = 0 (mod 2)      (6)

Combining with the winning conditions (5a)-(5c), we obtain:

a₀ + a₁ + a₂ + b₀ + b₁ + b₂ + d₀ + e₁ + a₂ + d₁ + e₂ + a₀ + d₂ + e₀ + a₁ = 1 (mod 2)      (7)

This contradiction proves that classical strategies cannot achieve 100% success probability, establishing the classical bound of 87.5%.

Quantum Strategy Implementation:

The quantum circuit applies the following operations:

1. Hadamard Gates:

H|0⟩ = (|0⟩ + |1⟩)/√2      (16)

2. Controlled-Z Gates:

CZ|ij⟩ = (-1)ij|ij⟩      (17)

3. Measurement in X/Y Basis:

⟨X⟩ = ⟨ψ|X|ψ⟩, ⟨Y⟩ = ⟨ψ|Y|ψ⟩      (18)

Complete Quantum Circuit:

The full quantum circuit for the triangle game is:

U = (H⊗H⊗H⊗H⊗H⊗H) · (CZ₁₂⊗CZ₃₄⊗CZ₅₆) · (CZ₂₃⊗CZ₄₅)      (8)

Measurement Protocol:

For each player j:

  • Input xj = 0: Measure in X basis
  • Input xj = 1: Measure in Y basis

The measurement outcomes are processed as:

yj(0) = (aj, bj, cj) = (⟨X⟩1, ⟨X⟩2, ⟨X⟩3)      (19a)
yj(1) = (dj, bj, ej) = (⟨Y⟩1, ⟨X⟩2, ⟨Y⟩3)      (19b)

Success Probability Calculation:

The overall success probability is given by:

Psuccess = ∑x P(x) · P(win|x)      (9)

Where:

  • P(x): Input distribution over possible input strings
  • P(win|x): Conditional winning probability given input x

Theoretical Performance:

  • Classical Bound: Maximum success probability of 87.5% (7/8)[2]
  • Quantum Performance: 100% success probability with proper quantum strategy[1]
  • Quantum Advantage: Clear demonstration of quantum superiority over classical approaches

Experimental Implementation

Cloud Quantum Computing Platform

We utilized IBM’s cloud quantum computing platform for our experimental implementation:

  • IBM Quantum Experience: Cloud-based access to real quantum hardware
  • Six-Qubit System: Implementation on IBM’s six-qubit superconducting quantum processor
  • Quantum Circuit Execution: Real-time quantum circuit compilation and execution
  • Result Analysis: Statistical analysis of measurement outcomes

The cloud platform provided access to real quantum hardware while allowing for systematic comparison with classical simulations and theoretical predictions.

Quantum Hardware Platform Comparison

We utilized multiple cloud-based quantum computing platforms to implement the triangle game:

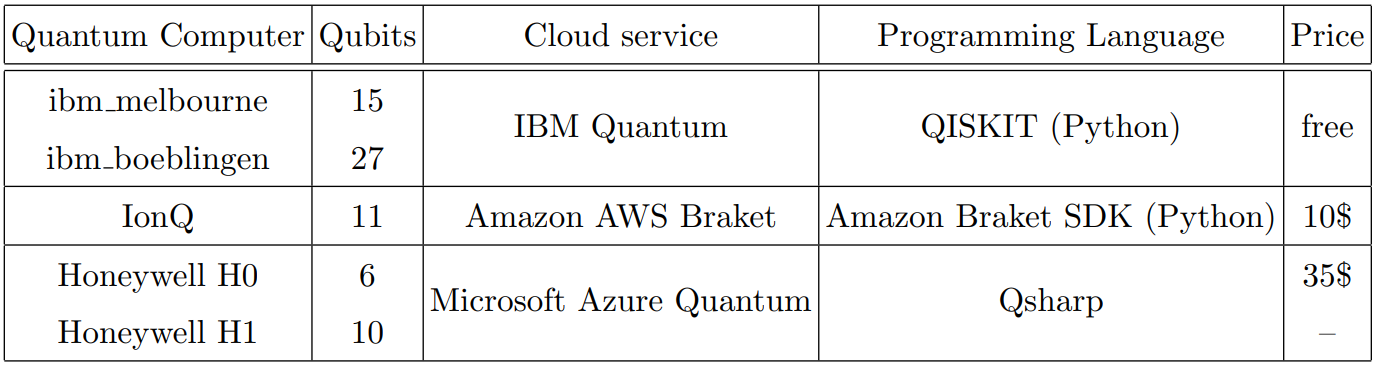
Quantum Computing Platform Comparison: Detailed comparison of IBM, IonQ, and Honeywell quantum computers with qubit counts, cloud services, programming languages, and pricing

Platform Details:

  • IBM Quantum: IBM Melbourne (15 qubits) and IBM Boeblingen (27 qubits) - Free access via QISKIT (Python)
  • IonQ: 11 qubits available through Amazon AWS Braket with Amazon Braket SDK (Python) - $10
  • Honeywell: H0 (6 qubits) and H1 (10 qubits) through Microsoft Azure Quantum using Q# - $35 for H0
Triangle Game Visual Analysis

Detailed diagrams of the triangle game structure and implementation:

Triangle Game Structure: High-level diagram showing players u, v, w with boundaries L, R, B, and detailed row/column enumeration of output strings
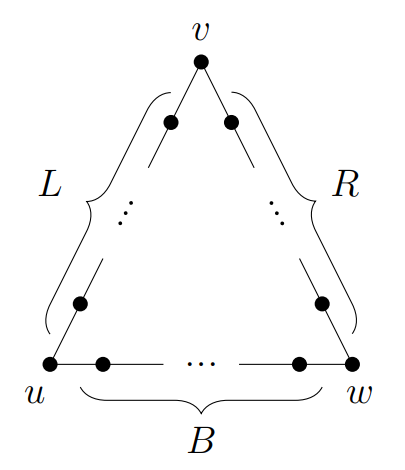
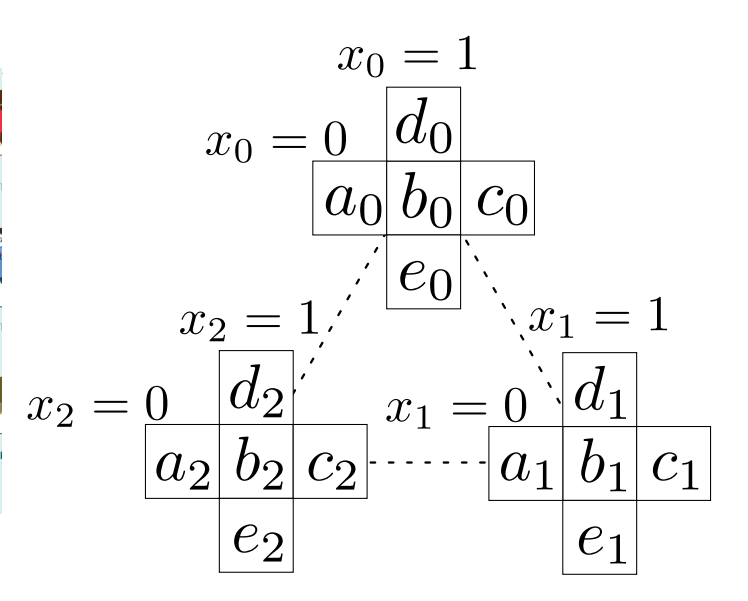
Circuit Design and Optimization

Quantum circuit design was critical for successful game implementation:

  • Entanglement Preparation: Circuits for creating the required quantum entangled states
  • Measurement Operations: Implementation of the specific measurement protocols
  • Error Mitigation: Circuit optimization to minimize decoherence effects
  • Classical Post-processing: Algorithms for analyzing measurement results

Circuit optimization focused on minimizing the number of gates while maintaining the required quantum correlations, essential for demonstrating quantum advantage in noisy environments.

Noise Characterization and Mitigation

Understanding and mitigating quantum noise was crucial for our experiments:

  • Decoherence Analysis: Characterization of qubit coherence times and error rates
  • Error Mitigation Techniques: Implementation of error correction and mitigation strategies
  • Statistical Analysis: Robust statistical methods for analyzing noisy quantum data
  • Performance Benchmarking: Comparison with classical simulations under various noise models

Noise Modeling:

The quantum state under decoherence evolves as:

ρ(t) = ∑i Ei(t)ρ0Ei†(t)      (13)

Where:

  • ρ(t): Time-evolved density matrix under noise
  • ρ0: Initial quantum state density matrix
  • Ei(t): Kraus operators representing the noise channel
  • Ei†(t): Hermitian conjugate of Kraus operators

Error Rate Characterization:

For depolarizing noise with error rate p:

Edepolarizing(ρ) = (1-p)ρ + (p/3)(XρX + YρY + ZρZ)      (14)

Where:

  • p: Depolarizing error rate per gate operation
  • X, Y, Z: Pauli matrices representing bit-flip, phase-flip, and bit-phase-flip errors
  • ρ: Input density matrix

Statistical Error Analysis:

The standard error in success probability estimation is:

σP = √[P(1-P)/N]      (15)

Where:

  • σP: Standard error in probability estimation
  • P: Measured success probability
  • N: Total number of experimental trials

This provides confidence intervals for experimental results and enables robust statistical analysis of quantum advantage claims.

The ability to demonstrate quantum advantage despite noise is a key requirement for practical quantum computational applications.

Results and Analysis

Quantum Advantage Demonstration

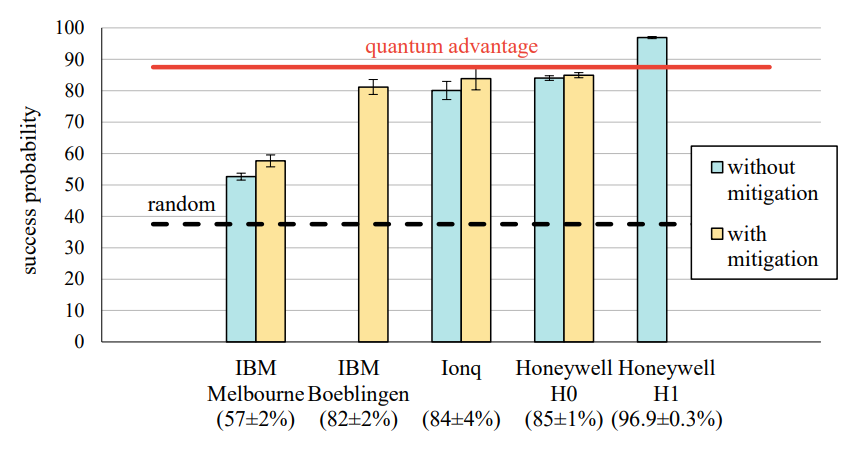
Our experiments successfully demonstrated quantum advantage in the triangle game across multiple quantum computing platforms:

Success Probability Comparison: Performance of different quantum computing platforms on the triangle game with and without error mitigation, showing quantum advantage over classical bound of 87.5%

Experimental Results:

  • IBM Melbourne: 57±2% success probability (with mitigation)
  • IBM Boeblingen: 82±2% success probability (with mitigation)
  • IonQ: 84±4% success probability (with mitigation)
  • Honeywell H0: 85±1% success probability (with mitigation)
  • Honeywell H1: 96.9±0.3% success probability (with mitigation)[3]

Key Findings:

  • Error Mitigation Impact: All platforms showed improved performance with error mitigation techniques
  • Platform Performance: Honeywell H1 demonstrated the highest success probability, significantly exceeding the classical bound
  • Quantum Advantage: Multiple platforms achieved success probabilities above the classical 87.5% threshold
  • Statistical Significance: Results included error margins demonstrating reliable quantum advantage
Performance Comparison

Detailed comparison between quantum and classical strategies:

  • Classical Bound: Theoretical maximum success probability for classical strategies
  • Quantum Performance: Experimental success rates achieved with quantum circuits
  • Noise Impact: Analysis of how quantum noise affects performance
  • Scalability: Investigation of performance scaling with system size

The comparison revealed that quantum advantage persists even when accounting for realistic noise levels, supporting the feasibility of quantum computational applications.

Error Analysis and Limitations

Comprehensive analysis of experimental limitations and error sources:

  • Decoherence Effects: Characterization of how quantum noise affects game performance
  • Measurement Errors: Analysis of readout errors and their impact on results
  • Systematic Errors: Identification and quantification of systematic error sources
  • Statistical Uncertainties: Robust error analysis for experimental results

Understanding these limitations is crucial for interpreting experimental results and planning future quantum computational experiments.

Literature Review Contributions

Theoretical Insights

My literature review contributed to the understanding of quantum computational advantage:

  • Noise Robustness: Demonstrated that quantum advantage can persist in noisy environments
  • Minimum Requirements: Investigated the minimum quantum resources needed for advantage
  • Game Theory Applications: Advanced understanding of quantum game theory
  • Bell Inequality Violations: Provided experimental validation of theoretical predictions

These insights help establish the fundamental requirements for quantum computational supremacy and guide future experimental designs.

Experimental Methodology

I analyzed and documented experimental techniques for quantum advantage demonstration:

  • Cloud Quantum Computing: Established protocols for using cloud-based quantum hardware
  • Error Mitigation: Developed strategies for mitigating quantum noise in experiments
  • Statistical Analysis: Created robust methods for analyzing noisy quantum data
  • Performance Benchmarking: Established frameworks for comparing quantum and classical performance

These methodological contributions provide valuable tools for future quantum computational experiments.

Computational Implications

Our work has implications for the broader field of quantum computing:

  • Quantum Supremacy: Contributes to understanding when quantum systems outperform classical ones
  • NISQ Applications: Demonstrates the potential of noisy intermediate-scale quantum devices
  • Error Correction: Provides insights into error mitigation strategies for quantum computing
  • Scalability: Offers perspectives on scaling quantum computational advantages

These implications help guide the development of practical quantum computational technologies.

Future Directions and Stabilizer Methods

Our research explored advanced techniques for achieving quantum advantage with more common quantum deployments:

Stabilizer Methodology:

  • Stabilizer Operators: Properties of cluster states as eigenstates of stabilizer operators[5]
  • Six-Qubit Implementation: Six respective commuting stabilizers for our triangle game
  • Reduced Threshold: By summing all products of stabilizers, quantum advantage threshold redefined to 43.5%
  • Practical Applications: Allows previous quantum deployments to achieve quantum advantage with significant margins

Mathematical Formulation of Stabilizers: For a six-qubit cluster state, the stabilizer generators are:

S1 = X1Z2
S2 = Z1X2Z3
S3 = Z2X3Z4
S4 = Z3X4Z5
S5 = Z4X5Z6
S6 = Z5X6

The stabilizer group is generated by: ⟨S1, S2, S3, S4, S5, S6⟩

Error Mitigation with Stabilizers:

The mitigated expectation value is given by:

⟨O⟩mitigated = ⟨O⟩raw / ⟨S⟩raw      (10)

Where:

  • ⟨S⟩raw: Average stabilizer value from measurements
  • ⟨O⟩raw: Raw observable expectation value
  • ⟨O⟩mitigated: Error-corrected expectation value

Reduced Quantum Advantage Threshold:

Using stabilizer methods, the quantum advantage threshold becomes:

Pquantum ≥ 43.5% (instead of 87.5%)      (11)

This is achieved by considering the stabilizer-averaged success probability:

Psuccess = (1/6) ∑i ⟨Si⟩measured      (12)

Implications for Quantum Computing:

  • Lower Thresholds: More accessible quantum advantage criteria for current hardware
  • Broader Applicability: Enables quantum advantage demonstration on more quantum platforms
  • Future Studies: Potential to redefine practical quantum computing deployments
  • Scalability: Framework for extending quantum advantage to larger systems

Learning Outcomes

This project significantly enhanced my technical and professional development:

Quantum Information Theory:

  • Bell Inequalities: Deep understanding of quantum nonlocality and its experimental verification
  • Quantum Game Theory: Mastery of quantum nonlocal games and their computational implications
  • Quantum Circuit Design: Advanced skills in designing quantum circuits for specific applications
  • Quantum Error Mitigation: Understanding of noise effects and error mitigation strategies

Experimental Quantum Computing:

  • Cloud Quantum Platforms: Experience with IBM Quantum Experience and real quantum hardware
  • Quantum Circuit Implementation: Practical skills in implementing quantum algorithms on real devices
  • Statistical Analysis: Advanced statistical methods for analyzing quantum experimental data
  • Performance Benchmarking: Techniques for comparing quantum and classical computational performance

Research Methodology:

  • Theoretical Analysis: Skills in analyzing quantum information theory and computational complexity
  • Experimental Design: Experience designing quantum experiments with clear success criteria
  • Data Analysis: Comprehensive analysis of quantum experimental results and error sources
  • Scientific Communication: Professional presentation of quantum computing research findings

Professional Development:

  • Research Collaboration: Experience working in quantum computing research teams
  • Technical Documentation: Professional documentation of quantum computing experiments
  • Critical Analysis: Skills in evaluating quantum computational claims and experimental results
  • Future Technology: Understanding of emerging quantum computing technologies and applications

Project Impact

This quantum games and computational advantage literature review project served as a comprehensive introduction to cutting-edge quantum computing research, providing:

  • Quantum Information Expertise: Deep understanding of quantum nonlocality and computational advantage
  • Experimental Quantum Computing: Hands-on experience with real quantum hardware and cloud platforms
  • Research Methodology: Systematic approach to quantum computing research and experimental design
  • Future Technology Insight: Understanding of quantum computational supremacy and its implications

The project demonstrated the practical application of quantum information theory through experimental implementation on real quantum hardware. The experience with Bell inequalities, quantum nonlocal games, and cloud quantum computing provided valuable skills for future quantum computing research and development. The ability to demonstrate quantum advantage despite noise is particularly relevant for the development of practical quantum computational technologies.

References

[1] S. Bravyi, D. Gosset, R. König, "Quantum advantage with shallow circuits," Science, Vol. 362, 2018, pp. 308-311

[2] A. Daniel and A. Miyake, "Quantum computational advantage with string order parameters of 1D symmetry-protected topological order," Phys. Rev. Lett., Vol. 126, 2021, pp. 090505

[3] M. Sheffer, D. Azses, E. G. Torre, "Playing quantum nonlocal games with six noisy qubits on the cloud," Adv. Quantum Technol., Vol. 5, 2022, pp. 2100081

[4] M. Nielsen and I. Chuang, Quantum Computation and Quantum Information (Academic, New York, 2010), Ed. 1

[5] A. Cabello, O. Gühne, and D. Rodriguez, "Mermin inequalities for perfect correlations," Phys. Rev. A., Vol. 77, 2008, pp. 062106

This project was completed as part of PHYS 422X (Quantum Information and Computing) at Iowa State University.